PAPER:
The use of statistical tests to
calibrate the Black-Scholes asset dynamics model
applied to pricing options with uncertain volatility
Lorella Fatone, Francesca Mariani, Maria Cristina Recchioni, Francesco Zirilli
1. Abstract
2. Introduction
3. The
calibration problem for the Black-Scholes model
4. Option
prices with uncertain volatility and statistical significance
5. Numerical
experiments (Animations
1, 2 )
6. References
1.
Abstract
A new method to solve the calibration problem for the Black-Scholes asset price dynamics model is proposed. The data
used in the calibration problem are the observations of the asset price on a
finite set of equispaced (known) discrete time
values. Statistical tests are used to obtain estimates with statistical
significance of the two parameters of the Black-Scholes
model, that is of the volatility and of the drift. The
consequences of these estimates on the option pricing problem are investigated.
In particular the pricing problem for options with uncertain
volatility in the Black-Scholes framework is
revisited and a statistical significance is associated to the price intervals
determined using the Black-Scholes-Barenblatt (BSB) equations. Numerical experiments with
synthetic and real data are presented. The real data considered are the daily
closing values of the S&P500 index and of the associated European call and
put option prices in the year 2005. The method proposed to calibrate the Black-Scholes dynamics model can be extended to other models
defined as stochastic dynamical systems used in science and engineering. A
detailed exposition of the material summarized in this website can be found in [10]. A general reference to the work of the authors and of their coauthors
in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
· The
research reported in this paper is partially supported by MUR - Ministero Università e Ricerca (
· The
numerical experience reported in this paper has been obtained using the
computing grid of ENEA (Roma, Italy). The support and sponsorship of ENEA are
gratefully acknowledged.
2. Introduction
The Black-Scholes
formulae [3] used to price European call
and put options are based on an asset price dynamics model. This model is a
stochastic dynamical system written as a stochastic differential equation. The
solution of this model is a stochastic process called geometric Brownian
motion. The model contains two real parameters: the volatility and the drift.
The Black-Scholes formulae depend on the volatility
parameter. The knowledge of the values of the volatility and of the drift is
necessary to use the model to forecast asset and options prices. Therefore in
practical circumstances the values of these parameters must be determined
before using the Black-Scholes dynamics model and the
option pricing formulae derived from it. That is, starting from the available
data, the problem of finding estimates of the parameters appearing in the asset
price dynamics model must be considered. This problem is called calibration
problem and is an inverse problem for a stochastic dynamical system defined by
a stochastic differential equation. The estimated parameter values, obtained
solving the calibration problem, are used to forecast the asset price at future
times and to evaluate the option pricing formulae instead than the “true”
(unknown) parameter values. We can conclude that the “accuracy” and the
reliability of the estimated parameter values concur to determine the accuracy
and the reliability of the asset prices forecasted and of the option prices
computed and/or forecasted.
Note that in recent years the validity of the asset
price dynamics model proposed by Black and Scholes in
1973 [3] has been disputed in the mathematical finance
literature and that several more refined models, such as, for example, [11], have been introduced to describe the asset price dynamics.
Nevertheless the Black-Scholes asset dynamics model
and particularly the option pricing formulae derived from it remain widely used
in the common practice of the financial markets. We will see in Section 3 and 4
that for the Black-Scholes model the solution of the
calibration problem using statistical tests and the investigation of its
consequences in the option pricing problem can be done easily using elementary
mathematics. For this reason the Black-Scholes asset
dynamics model is the natural choice to begin our study on the solution of
calibration problems for stochastic dynamical systems using statistical tests.
The data used in the calibration problem are the observations
of the asset price on a finite set of equispaced
(known) discrete time values. We show how to use elementary statistical tests
(that is the Student's T and the c2 tests) in order to provide values of the drift and of
the volatility parameters of the Black-Scholes model
with a statistical significance associated. For the convenience of the reader
we recall that in a statistical test the statistical significance a, 0 < a < 1, is the maximum
probability of rejecting the (null) hypothesis of the test when the hypothesis
is true. Let us describe more in detail the work summarized in this website and
presented in [10].
As already mentioned the solution of the Black-Scholes asset price dynamics model is a stochastic process
called geometric Brownian motion depending from two parameters, the drift and
the volatility. From this fact it follows that the asset price at any given
time is modeled as a random variable with log-normal distribution and therefore
the log-return of the asset price is normally distributed. Moreover it is easy
to see that the asset price log-return increments associated to observations of
the asset price made on a (finite) set of equispaced
time values are a sequence of values sampled from a set of independent
identically distributed Gaussian random variables. The mean and the variance of
these Gaussian random variables can be written with elementary formulae as a
function of the drift and of the volatility parameters of the Black-Scholes asset price dynamics model and of the time interval
between the observations. That is, starting from a sample of observations of
the log-return increments on a finite set of equispaced
(known) time values it is possible using elementary statistical tests (i.e.:
Student's T and c2 tests) to
estimate, with a given (statistical) significance, the mean and the variance of
the Gaussian random variables associated to the log-return increments. In fact
the Student's T test ([15], [16]) is the test used to establish with statistical significance whether
the mean of a normally distributed population made of independent samples has a
value or belongs to an interval specified in a “null” hypothesis. Similarly the
c2 test ([14], [16]) is the test used to
establish with statistical significance whether the variance of a normally
distributed population made of independent samples has a value or belongs to an
interval specified in a “null” hypothesis. Moreover from the knowledge of the
parameters of the Gaussian random variables associated to the log-return
increments derived from the statistical tests it is easy to recover the
corresponding knowledge of the parameters of the Black-Scholes
model and to associate to it a statistical significance.
The use of statistical tests in the solution of the
calibration problem for stochastic dynamical systems, such as the Black-Scholes model, is an interesting way of approaching these
inverse problems that can be used elsewhere in mathematical finance and in many
application contexts different from mathematical finance. The significance
levels obtained for the parameter values (intervals) of the Black-Scholes model are relevant in many practical circumstances.
In Section 4 we consider one of these circumstances: the
pricing problem for options with uncertain volatility. The pricing problem for
options with uncertain volatility has been considered by several authors in the
scientific literature. For simplicity we refer to [1] and [13] where, in the Black-Scholes framework, assuming that the (uncertain) volatility
belongs to a known interval, the corresponding price intervals for the
(European vanilla) option prices are determined using the Black-Scholes-Barenblatt (BSB) equations. Thank to our methodology statistical
significance levels can be attributed to the option price intervals determined
using the BSB equations.
Finally the results obtained in the calibration
problem for the Black-Scholes model are applied to
the study of synthetic and real data. The synthetic data considered are
generated integrating numerically the stochastic differential equation that
defines the asset price dynamics in the Black-Scholes
model for several choices of the parameter values. The real data studied are
the time series of the daily closing values of the S&P500 index and of the
associated European vanilla option prices in the year 2005. The numerical
results obtained are computationally simple and statistically convincing.
In mathematical finance the problem of estimating the
volatility of the asset price starting from a time series of observed data
(asset and/or option prices) has received great attention. The most common
methods used in the literature are: the implied and the historical (or
realized) volatility methods. The approach proposed here to solve this problem
is different from these methods. Unlike in the implied volatility method we do
not consider the volatility implied by the option prices observed in the
market. That is we don't estimate the volatility parameter of the asset price
using as data the prices of a variety of options on the asset with different
strikes and expiration dates. On the other hand, as in the historical
volatility method, our method estimates the volatility starting from the asset
prices observed on a finite set of discrete time values. Our method improves
with respect to the historical volatility method since associates a
significance level to the volatility estimate obtained. In some sense going
from the historical volatility method to the method proposed here corresponds
to going from the use as volatility estimate of the “sample volatility” to the
use of a statistical test (i.e. the c2 test) tailored on the random variable whose
parameters must be estimated. That is, roughly speaking, it corresponds to going
from a method of descriptive statistics to a method of mathematical statistics.
Let us mention some valuable features of the work presented here.
First of all the idea proposed is very simple. Although the idea is introduced
in the context of the Black-Scholes model, it can be
applied to other stochastic dynamical systems used in mathematical finance to
describe asset price dynamics. For example we have in mind the Heston model (see [11], [4] [6]), or some of its variations such as the models introduced in [5], [7], [8], [9] to study some specific
problems. In [4], [5], [6], [7], [8], [9] the calibration problem for the models considered is studied using the
“implied volatility method” or the maximum likelihood method. In those papers
there are not statistical tests involved in the solution of the calibration
problems and to the estimated parameter values no statistical significance is
associated. Note that in the study of the calibration problem for these models,
or, more in general, for a generic stochastic dynamical system no elementary
statistical tests (such as Student's T and c2 tests) can be used. In order to extend the method
suggested here to the study of these more general dynamical systems new ad hoc
statistical tests must be developed. Most likely in order to carry out these
new statistical tests on a data sample a substantial use of numerical methods
will be necessary.
A general reference to the work of the authors and of
their coauthors in mathematical finance is the website: http://www.econ.univpm.it/recchioni/finance.
The reader not interested in
mathematical details may jump to Section 5.
3. The calibration problem for the
Black-Scholes model
Let St > 0 denote the asset price at time t ³ 0. The Black-Scholes model [3] assumes that St, t
> 0, is a stochastic process whose
dynamics is governed by the following stochastic differential equation:
![]()
![]() , (2)
, (2)
where m, s are real parameters, m is the drift, s > 0 is the volatility, Wt,
t > 0, is the standard Wiener process, W0
= 0, dWt, t > 0, is its stochastic differential
and the initial condition ![]() > 0 is a given random variable. For simplicity we assume
that
> 0 is a given random variable. For simplicity we assume
that ![]() is a random variable concentrated in a point with
probability one, and, with abuse of notation, we denote this point with
is a random variable concentrated in a point with
probability one, and, with abuse of notation, we denote this point with ![]() > 0. The parameters m, s are the unknowns of the calibration
problem.
> 0. The parameters m, s are the unknowns of the calibration
problem.
The stochastic differential
equation (1) defines the so
called geometric Brownian motion. Let ln(·) denote
the logarithm of ·, for t ³ 0 the quantity ![]() is called log-return at time t of
the asset whose price is St. It is easy to see that the Black-Scholes asset price log-return increments associated to a
discrete set of equispaced time values are a sequence
of independent identically distributed Gaussian random variables. In particular
let Dt >
0 be a time increment and let ti = i Dt, i = 0,1,¼,n, be a discrete set of equispaced time
values that later will be chosen as the set of the observation times. We define
is called log-return at time t of
the asset whose price is St. It is easy to see that the Black-Scholes asset price log-return increments associated to a
discrete set of equispaced time values are a sequence
of independent identically distributed Gaussian random variables. In particular
let Dt >
0 be a time increment and let ti = i Dt, i = 0,1,¼,n, be a discrete set of equispaced time
values that later will be chosen as the set of the observation times. We define ![]() , the asset price log-return increment when t goes from
, the asset price log-return increment when t goes from ![]() to ti as follows:
to ti as follows:
![]()
It is easy to see (see [10] for more details) that the random variables ![]() ,, i = 1,2,¼,n, are independent identically
distributed Gaussian random variables with mean M and variance V2
where:
,, i = 1,2,¼,n, are independent identically
distributed Gaussian random variables with mean M and variance V2
where:
![]()
We consider the following
calibration problem: given Dt > 0, a statistical
significance level a, 0 < a < 1, and
the asset price ![]() observed at time t = ti = i Dt, i = 0,1,¼,n, determine two intervals where the parameters m and s of the model (1) respectively belong with the given significance level a.
observed at time t = ti = i Dt, i = 0,1,¼,n, determine two intervals where the parameters m and s of the model (1) respectively belong with the given significance level a.
The observations![]() of the asset price at time t = ti, i = 0,1,¼,n, are non negative real numbers that we assume not affected by errors.
These n+1 observations of the asset price and the corresponding time values are
the data used in the calibration problem. The observed log-return increments
of the asset price at time t = ti, i = 0,1,¼,n, are non negative real numbers that we assume not affected by errors.
These n+1 observations of the asset price and the corresponding time values are
the data used in the calibration problem. The observed log-return increments ![]() , i = 1,2,¼,n, are a sample of n observations taken respectively from
, i = 1,2,¼,n, are a sample of n observations taken respectively from ![]() , i = 1,2,¼,n, that is taken from a set of independent identically distributed
Gaussian random variables. Using this data sample, through the Student's T test
and the c2 test respectively (see [14], [15], [16]), we determine two
intervals where the mean M and the variance V2 of the Gaussian
random variables mentioned above belong with the given significance level a. From the knowledge of the intervals determined for M and V2,
the corresponding intervals for m and s can be recovered
inverting the relations (4).
, i = 1,2,¼,n, that is taken from a set of independent identically distributed
Gaussian random variables. Using this data sample, through the Student's T test
and the c2 test respectively (see [14], [15], [16]), we determine two
intervals where the mean M and the variance V2 of the Gaussian
random variables mentioned above belong with the given significance level a. From the knowledge of the intervals determined for M and V2,
the corresponding intervals for m and s can be recovered
inverting the relations (4).
In particular given a
significance level a, 0 < a < 1, we can
perform statistical tests on the variance V2 and on the mean M of
the random variables ![]() i = 1,2,¼,n, starting from the data sample
i = 1,2,¼,n, starting from the data sample ![]() , i = 1,2, ¼,n, using the c2 test and the
Student's T test respectively. This implies that given a, 0 < a < 1, and
given four real numbers
, i = 1,2, ¼,n, using the c2 test and the
Student's T test respectively. This implies that given a, 0 < a < 1, and
given four real numbers ![]() such that
such that ![]() we can accept or reject, with
significance level a, the hypotheses:
we can accept or reject, with
significance level a, the hypotheses:
![]() ,
,
![]() , (5)
, (5)
and, consequently, using the relations (4) , we can accept or reject, with significance level a, the hypotheses:
![]() ,
, ![]() (6)
(6)
![]() ,
and
,
and ![]() (7)
(7)
Relations (7) are obtained simply translating to s and m the results on V2 and M
obtained with the statistical tests. For more details see [10].
To estimate V2 and
M from the log-return increments we must choose the hypotheses to test. This
can be done in many ways. The results on synthetic and real data shown in Section 5 are obtained using
a set of heuristic rules to choose the hypotheses to be tested. These rules and
the way of using them is defined in the Procedures 1 and 2 described in detail
in [10].
4. Option prices with uncertain volatility and statistical
significance
Let us consider the Black-Scholes asset price dynamics model (1) and the problem of pricing options with uncertain
volatility in the Black-Scholes model with a given
statistical significance a, 0 < a < 1. We assume that the volatility
value s is not known exactly, but that it
is known that the volatility lies in a specified range, let us say s1 £ s £ s2, where s1, s2 are constants and 0 < s1 < s2, with a given significance level a. In fact, using the c2 test on the data of the calibration
problem posed in Section 3, we can decide whether to accept or
to reject the statement:
|
(8) |
We limit our attention to
European vanilla call and put options.
The question that we want to
answer is: given a significance level a, 0 < a < 1,
assuming that the hypothesis
s1
£ s
£ s2 is accepted with
significance level a, determine the corresponding range where the value of an European
vanilla option lies (with significance level a). The answer to this question
follows from the work of Avellaneda, Levy and Parás [1] and of Lyons [13]. These authors
propose a way to price options in the Black-Scholes
model when the volatility s is not known exactly, but it is simply known that:
|
(9) |
In [1]
and [13] significance levels are not considered. We remark that the
bounds s1 and s2 in the two equations (8) and (9) are determined in
different ways. In (8) they are
parameters that can be chosen together with a significance level in such a way
that on the data sample considered the c2 test will accept
the hypothesis s1
£ s
£ s2 with significance
level a, or are parameters
determined starting from the data sample through an iterative procedure such as
Procedure 1 described in [10]. In (9) these bounds are
assigned using common sense assumptions or they are determined either looking
at extreme values of the volatility implied by the observed option prices or
looking at the low-high peaks of the historical volatility.
Let t be the time variable, S
be the asset price, τ> 0 be the expiration date of the option to be priced. In [1] and [13] it is shown that, in the Black-Scholes framework, when the volatility satisfies (9), there exists an
interval [Ʋ1, Ʋ2] depending on S
and t, such that the price Ʋ = Ʋ(S,t),
S > 0, 0 <
t £ τ, of the option lies in this interval, that is (9) implies that:
|
The worst-case option value Ʋ1(S,t), S > 0,
0 < t £ τ, and the best-case option value Ʋ2(S,t), S
> 0, 0 < t £ τ, satisfy two nonlinear partial differential equations known as Black-Scholes-Barenblatt (BSB)
equations. The BSB equations reduce to the usual Black-Scholes
equation when there is no uncertainty about the volatility value (i.e. in the
case s1 = s2). For a general pay-off function
the BSB equations do not have a closed-form solution and must be solved
numerically. However due to the properties of the BSB equations when a call or
a put option is considered, the BSB equations reduce to the Black-Scholes equation. See [1] and [13] for more details. We briefly recall that the Black-Scholes equation is linear and, when simple final conditions,
as the ones corresponding to call and put options, are imposed, can be solved
explicitly leading to the Black-Scholes formulae (see
[3]).
Now we can answer the question
posed at the beginning of this Section. First of all let us assume that a
“true” value of the volatility s exists even if it is unknown. From the fact that in the Black-Scholes model the price Ʋ of an option is a
monotonically increasing function of the volatility s we can conclude that when (8) holds we have:
|
(11) |
where Ʋ1(S,t), Ʋ2(S,t),
S > 0, 0 < t < τ, are the solutions of the appropriate BSB equations.
The meaning of the sentence (11) can be restated
as follows: if we assume that a “true” value of the volatility s exists and that based on the analysis of a data sample we accept the
hypothesis that this true value lies in the range [s1, s2] with significance
level a, i.e. s1 £
s £
s2 with probability 1-a, it follows that the corresponding “true” value of the option price Ʋ
lies in the range [Ʋ1, Ʋ2] with
probability 1-a, i.e. “Ʋ1(S,t) £
Ʋ(S,t)
£ Ʋ2(S,t), S >
0, 0 < t < τ, with
significance level a”, where Ʋ1, Ʋ2, are
the solutions of the appropriate BSB equations.
5. Numerical experiments
Let us discuss some
numerical experiments. The first numerical experiment presented consists in
solving the calibration problem discussed in Section 3 using synthetic data. In this experiment the analysis of a time series
of daily data of the asset prices during a period of ten years is considered.
We assume that a year is made of 253 trading days. The time series studied is
made of 253·10+1=2531 daily asset price data, that is it is made of the asset
price ![]() observed at time t = ti = i Dt, i = 0,1,¼, 2530, Dt = 1/253. These synthetic data have been obtained computing one
trajectory of the stochastic differential equation (1) for several choices of the parameter values and looking at the
computed trajectory at time t = ti = i Dt, i = 0,1,¼, 2530. We have chosen as initial condition at time t = t0 =
0, S0 =
observed at time t = ti = i Dt, i = 0,1,¼, 2530, Dt = 1/253. These synthetic data have been obtained computing one
trajectory of the stochastic differential equation (1) for several choices of the parameter values and looking at the
computed trajectory at time t = ti = i Dt, i = 0,1,¼, 2530. We have chosen as initial condition at time t = t0 =
0, S0 = ![]() = 1200. We choose m =
= 1200. We choose m = ![]() = 0.01 and s =
= 0.01 and s = ![]() = 0.1 in the first five years of
data (i.e. when t = ti, i = 0,1,¼,1264), m =
= 0.1 in the first five years of
data (i.e. when t = ti, i = 0,1,¼,1264), m =![]() = 0.06 and s =
= 0.06 and s = ![]() = 0.4 in the sixth and seventh year of data (i.e. when t = ti, i = 1265,1266,¼,1770) and m =
= 0.4 in the sixth and seventh year of data (i.e. when t = ti, i = 1265,1266,¼,1770) and m = ![]() = 0.03 and s =
= 0.03 and s = ![]() = 0.2 in the last three years of data (i.e. when t = ti,
i = 1771,1772¼,2530). The synthetic data are generated using as initial value of the
sixth year of data the last datum of the fifth year of data. A similar
statement holds for the initial value of the last three years of data. The
daily log-return increments of the synthetic asset prices generated in this way
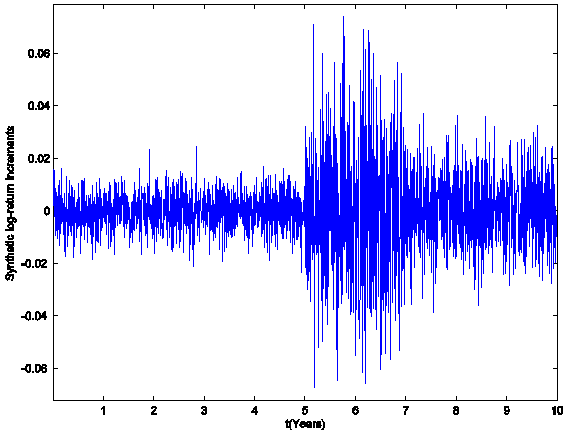
are shown in Figure 1. The fact that the data are generated using three
different choices of parameter values can be seen simply looking at Figure 1.
= 0.2 in the last three years of data (i.e. when t = ti,
i = 1771,1772¼,2530). The synthetic data are generated using as initial value of the
sixth year of data the last datum of the fifth year of data. A similar
statement holds for the initial value of the last three years of data. The
daily log-return increments of the synthetic asset prices generated in this way
are shown in Figure 1. The fact that the data are generated using three
different choices of parameter values can be seen simply looking at Figure 1.
Figure 1: The daily log-return
increments (synthetic data).
We consider the following
calibration problem: given Dt = 1/253, a = 0.1, and given the asset price observation ![]() at time t = ti = i Dt, i = 0,1,¼,2530, determine the intervals where the parameters m and s of model (1) belong with significance level a = 0.1.
at time t = ti = i Dt, i = 0,1,¼,2530, determine the intervals where the parameters m and s of model (1) belong with significance level a = 0.1.
We solve this calibration
problem with Procedures 1 and 2 described in [10] using the data
associated to a time window made of 253 consecutive observation times, that is
the observations corresponding to 253 consecutive trading days (one year), and
we move this window across the ten years of data discarding the datum corresponding
to the first observation time of the window and inserting the datum
corresponding to the next observation time after the window. The calibration
problem is solved for each choice of the data time window applying Procedures 1
and 2 described in [10], that is it is solved 2530-253+1=2278 times finding for each
calibration problem solved two intervals where the volatility and the drift
parameters respectively belong with significance level a = 0.1. The reconstructions of the parameters obtained moving the window
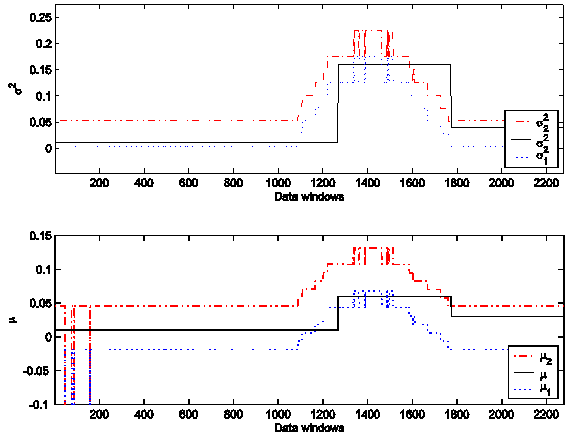
along the data as specified above are shown in Figure 2, Animation 1 and Animation 2. Figure 2, Animation 1 and Animation 2 show the “true”
values of the parameters and the intervals determined using the statistical
tests on the data windows via Procedures 1 and 2 of [10]. In particular Animation
1 (Animation 2) is a digital
movie showing the parameter s2 (m) reconstructed from the synthetic data. In Figure 2, Animation
1 and Animation 2 the abscissa
corresponds to the data window used to reconstruct the model parameters. The
data windows are numbered in ascending order beginning with one according to
the order in time of the first day of the window considered. In particular
Figure 2, Animation 1 and Animation 2 show that the
intervals containing the parameters m and s and the time when
the parameter values change are reconstructed satisfactorily.
Figure 2: The parameters s2 and m reconstructed from the synthetic
data.
Animation
1: click here to
download a digital movie showing the parameter s2 reconstructed from the synthetic
data.
Animation 2: click here to download a digital movie showing
the parameter m reconstructed from the synthetic
data.
The second numerical
experiment uses real data. The real data studied are the 2005 daily data of the
U.S. S&P500 index (see Figure 3) and of the prices of European vanilla call
and put options on this index.
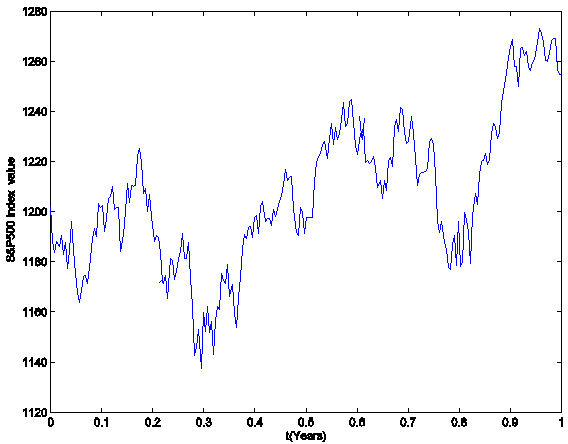
Figure 3: The S&P500 index (year
2005).
We remind that the
U.S. S&P500 index is one of the leading indices of the New York Stock
Exchange. More specifically we consider the daily closing values of the
S&P500 index and of the bid prices of the vanilla European call and put
options on the S&P500 index during the period of about 12 months going from
January 3, 2005 to December 30, 2005. In this period we have 253 trading days
and more than 153.000 option prices. We limit our study to the call and the put
prices corresponding to options that have a positive volume (i.e. a positive
number of contracts) traded the day corresponding to the price considered and a
positive bid price. These are 46.823 options prices. Since there are 253
trading days in the year 2005 we choose as time unit a “year” made of 253
trading days. We choose as time t = t0 = 0 the day January 3, 2005.
We have 253 daily S&P500 index values ![]() observed at time t = ti = i Dt, i = 0,1,¼,252, with Dt = 1/253 year. The S&P500 index and the corresponding (daily)
log-return increments in the year 2005 are shown in Figure 3 and Figure 4 respectively.
observed at time t = ti = i Dt, i = 0,1,¼,252, with Dt = 1/253 year. The S&P500 index and the corresponding (daily)
log-return increments in the year 2005 are shown in Figure 3 and Figure 4 respectively.
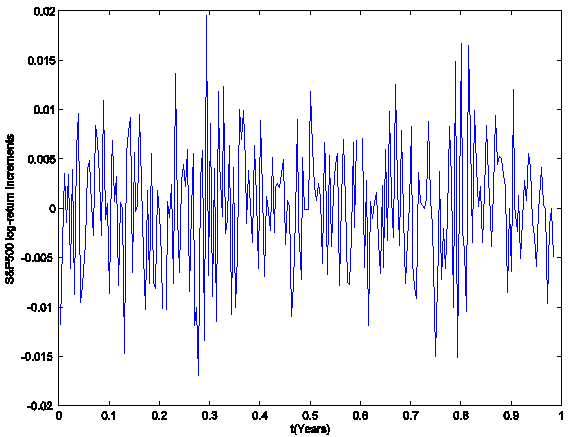
Figure 4: The S&P500 daily
log-return increments (year 2005).
We interpret this
set of data using the Black-Scholes model as
suggested in Section 3. We begin studying
the variance and the drift of the Black-Scholes model
used to explain S&P500 index during the year 2005. The S&P500 daily
log-return increments ![]() , i = 1,2,¼,252, are analyzed using the Black-Scholes
model, that is they are considered as a sample (see Figure 4) of 252
observations taken from a set of independent identically distributed Gaussian
random variables where the mean M and the variance V2 are defined in
(4). First we
estimate V2 (and therefore s2) using the c2 test and
subsequently we estimate M (and therefore m) using the Student's T test using Procedures 1 and 2 described in [10].
, i = 1,2,¼,252, are analyzed using the Black-Scholes
model, that is they are considered as a sample (see Figure 4) of 252
observations taken from a set of independent identically distributed Gaussian
random variables where the mean M and the variance V2 are defined in
(4). First we
estimate V2 (and therefore s2) using the c2 test and
subsequently we estimate M (and therefore m) using the Student's T test using Procedures 1 and 2 described in [10].
Given the data sample made of
the S&P500 daily log-return increments ![]() , i = 1,2,¼,252, the significance level a = 0.1, and appropriate initial values to start the Procedures 1 and 2
described in [10] we find that the
hypotheses:
, i = 1,2,¼,252, the significance level a = 0.1, and appropriate initial values to start the Procedures 1 and 2
described in [10] we find that the
hypotheses:
|
|
(13) |
are accepted with significance level a = 0.1.
Let us do a kind of stability
analysis of the intervals (12), (13) determined with
the statistical tests. To do this we fix a = 0.1 and we apply Procedures 1 and 2 described in [10] to determine the
intervals where s2 and m belong with significance level a starting from a window of 70 consecutive observations corresponding to
70 consecutive observation times (i.e. 70 consecutive trading days). As done
before we move the data window through the data time series discarding the
datum corresponding to the first observation time of the window and inserting
the datum corresponding to the next observation time after the window.
Proceeding in this way we have 252-70+1 data windows in the data time series
considered and for each one of these data windows we solve the corresponding
calibration problem. We find 252-70+1 couples of intervals where the volatility
and the drift parameter belong with significance level a = 0.1. Figure 5 shows that, changing the data window, the intervals
determined through Procedures 1 and 2 remain stable. In Figure 5 the abscissa
represents the data windows used to reconstruct the model parameters numbered
in ascending order beginning with one according to the order in time of the
first day of the window considered. In correspondence to each data window the
intervals determined by Procedures 1 and 2 of [10] are shown.
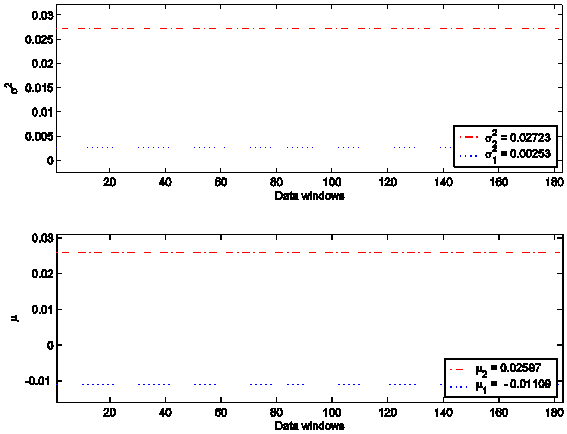
Figure 5: The parameters s2 and m reconstructed from the S&P500
data (year 2005).
Finally we consider
the 46.823 S&P500 European call and put option prices of the year 2005
already mentioned and we try to interpret them using the method developed in Section 4. From the
estimates (6) established with significance level a = 0.1, we are able to determine the corresponding option price
intervals using the BSB equations. That is we can determine the worst-case
option values Ʋ1(S,t),
S > 0, 0 <
t £ τ, and the best-case option values Ʋ2(S,t), S > 0, 0 < t £ τ. We compute the percentage of the prices of the European call (%
call) and put (% put) options on the S&P500 observed in the year 2005 that
verify (11) when we assume
the first relation in (6). The results obtained are shown in Tables 1-3. In
these tables Ncall and Nput
denote respectively the number of the call prices and of the put prices
corresponding to options whose characteristics are described in the caption of
the table. The quantities Icall and Iput denote respectively the average relative
amplitude of the call price intervals and of the put price intervals determined
using the BSB equations, and Pcall, Pput denote respectively the average bid price
of the call and of the put prices. In parentheses in the % call and % put
columns it is written the average number of contracts on the options considered
traded.
Table 1: S&P500 option prices:
in the money options (year 2005). These results are obtained using estimates (12), (13).
Table 2: S&P500 option prices:
at the money options (year 2005). These results are obtained using estimates
(14), (15).
Table 3: S&P500 option prices:
out of the money options (year 2005). These results are obtained using
estimates (16), (17).
We recall that
given the asset price S and the strike price K of an option, a call option (a
put option) is in the money if S > K (if S < K), is out the money if S < K (if S > K) and is at the money if S = K. In the numerical experiments the
condition S = K is substituted with |S-K| < e where e is a (given) positive quantity. As a consequence the conditions S >
K, S < K are rewritten as S > K+e, and S <
K-e, respectively. Using this criterion the 46.823 option prices considered
above are divided in three subsets corresponding to prices of in the money, at
the money and out of the money options. We take e equal to one per cent of the average strike price of the options considered.
Tables 1 refers to the in the money S&P500 option prices and it is obtained
specifying (6) as (12), (13).
A similar analysis relative to
S&P500 option prices corresponding to options out and at the money shows
that the use of the intervals (12), (13) leads to huge
call and put price intervals making the results obtained of dubious practical
value. One way of overcoming this drawback is to refine the estimates (12), (13) changing the
value of a tolerance parameter named tol used in
Procedures 1 and 2 described in [10] until option price intervals of “acceptable average relative amplitude”
(i.e. average relative amplitude of some tens of percentage points) are
obtained. For more details see [10]. Reducing by one quarter the parameter tol we
find that the hypotheses:
|
|
are accepted with significance level a = 0.1. The choice
of (14), (15) as intervals containing s2 and m respectively leads to average
relative amplitudes of some tens of percentage points for the option price
intervals when call and put options at the money are considered. Table 2 shows the results obtained on at
the money option prices using (14), (15).
When S&P500 option prices
relative to options out the money are considered it is necessary to reduce
further the parameter tol to keep the average
relative amplitude of the option price intervals to reasonable values. For
example reducing further the parameter tol we find
that the hypotheses:
|
|
are accepted with significance level a = 0.1. Table 3 shows the results obtained on out
of the money option prices using (16), (17).
Table 1 shows that the in the money S&P500 option prices are well
interpreted by the model proposed here. Percentages of the prices of the in the
money S&P500 call and put options explained by the model in the 60%-80%
range with average relative amplitude of the option price intervals in the
20%-40% range can be considered as a good result of possible practical value.
Looking at Table 1 we see that in the case of in the money options the call
prices seem to be better explained than the put prices. On the other hand if we
look at the numerical results shown in Table 2 we see that the at the money
S&P500 put options prices are better explained than the corresponding
S&P500 call options prices. Altogether also the results relative to at the
money S&P500 option prices are satisfactory. Unfortunately Table 3 shows
that the out of the money S&P500 option prices and above all the S&P500
prices relative to out of the money put options are not well interpreted using
our methodology. This could be related to the fact that the out of the money
options have usually low prices. Tables 1-3 show that the prices of the options out of the money are the smallest
ones.
6. References
[1] M.Avellaneda, A.Levy, A.Parás, “Pricing and hedging derivative securities in
markets with uncertain volatilities”, Applied Mathematical Finance, 2,
pp. 73-88, 1995.
[2] A.Azzalini, “A class of distributions which
includes the normal ones”, Scandinavian Journal of Statistics, 12(2),
pp. 171-178, 1985.
[3] F.Black, M.Scholes, “The pricing of
options and corporate liabilities”, Journal of Political Economy, 81,
pp. 637-659, 1973.
[4] F.Mariani, G.Pacelli, F.Zirilli,
“Maximum likelihood estimation of the Heston
stochastic volatility model using asset and option prices: an application of
nonlinear filtering theory, Optimization Letters, 2, pp. 177-222,
2008.
[5] L. Fatone, F.Mariani, M.C.Recchioni, F.Zirilli, “Maximum
likelihood estimation of the parameters of a system of stochastic differential
equations that models the returns of the index of some classes of hedge funds”,
Journal of Inverse and Ill Posed Problems, 15, pp. 493-526, 2007. (http://www.econ.univpm.it/recchioni/finance/w5).
[6] L.Fatone, F.Mariani, M.C.Recchioni, F.Zirilli, “The calibration of the Heston
stochastic volatility model using filtering and maximum likelihood methods”, in
Proceedings of Dynamic Systems and Applications, G.S.Ladde,
N.G.Medhin, Chuang Peng, M.Sambandham Editors, Dynamic Publishers, Atlanta, Georgia,
USA, 5, pp. 170-181, 2008. (http://www.econ.univpm.it/recchioni/finance/w6).
[7] L.Fatone, F.Mariani, M.C.Recchioni,
F.Zirilli, “An explicitly solvable multi-scale
stochastic volatility model: option pricing and calibration”, Journal of
Futures Markets, 29(9), pp. 862-893, 2009. (http://www.econ.univpm.it/recchioni/finance/w7).
[8] L.Fatone, F.Mariani, M.C.Recchioni, F.Zirilli, “Calibration of a multiscale
stochastic volatility model using as data European option prices”, Mathematical
Methods in Economics and Finance, 3, pp. 49-61, 2008.
[9] L.Fatone, F.Mariani, M.C.Recchioni,
F.Zirilli, “The analysis of real data using a multiscale stochastic volatility model”, European
Financial Management,doi: 10.1111/j.1468-036X.2010.00584.x, (2011). (http://www.econ.univpm.it/recchioni/finance/w9).
[10] L.Fatone, F.Mariani, M.C.Recchioni,
F.Zirilli, “The use of statistical tests to calibrate
the Black-Scholes asset dynamics model applied to
pricing options with uncertain
volatility”, Journal of Probability and Statistics, Volume 2012, Article ID 931609, 20 pages, 2012. (http://www.econ.univpm.it/recchioni/finance/w11).
[11] S.L.Heston, “A closed-form solution for options with stochastic volatility with
applications to bond and currency options”, The Review of Financial Studies,
6(1), pp. 327-343, 1993.
[12] J.H.Hull, Options, Futures, and Other Derivatives, 7th Edition, Pearson
Prentice Hall, London, 2008.
[13] T.J.Lyons, “Uncertain volatility and the risk-free synthesis of derivatives”, Applied
Mathematical Finance, 2(2), pp. 117-133, 1995.
[14] K.
Pearson, “On the criterion that a given system of deviations from the probable
in the case of correlated system of variables is such that it can be reasonably
supposed to have arisen from random sampling”, Philosophical Magazine, 50,
pp. 157-175, 1900.
[15] Student [W.S.Gosset*], “The probable
error of a mean”, Biometrika, 6(1), pp.
1-25, 1908.
[16] R.A.Johnson, G.K.Bhattacharyya, Statistics: Principles and Methods,
5th Edition, John Wiley & Sons, New York, 2006.
* From Wikipedia: “The T-statistic was
introduced in 1908 by William Sealy Gosset, a chemist
working for the Guinness brewery in Dublin, Ireland (“Student” was his pen
name). Gosset had been hired due to Claude Guinness's
innovative policy of recruiting the best graduates from Oxford and Cambridge to
apply biochemistry and statistics to Guinness' industrial processes. Gosset devised the T test as a way to cheaply monitor the
quality of stout. He published the test in Biometrika
in 1908, but was forced to use a pen name by his employer, who regarded the
fact that they were using statistics as a trade secret. In fact, Gosset's identity was unknown to fellow statisticians.”